티스토리 뷰
플로이드 워셜 알고리즘은 그래프에서 최단 거리를 구하는 알고리즘이다.
| 기능 | 장점 | 단점 |
| 모든 노드 간에 최단 경로를 탐색 | 음수 가중치 에지가 있어도 수행할 수 있음 | 속도가 느림 O(n3) |
플로이드 워셜 알고리즘을 사용할 때는 시간 복잡도를 반드시 고려해야 한다.
플로이드 워셜 알고리즘의 가장 핵심적인 원리는 A 노드 에서 B 노드를 거쳐 C노드로 갈때 ( A -> B -> C)
A 노드와 C노드의 경로가 최단 경로일때 (A -> B -> C) 중간 경로들인 A노드 에서 B (A -> B -> C)노드 까지 가는 경로도 최단 경로인 것이다.
D[A][C] = Math.min(D[A][C], D[A][B] + D[B][C])
A 에서 C까지의 최단 거리는
A 에서 C까지의 기존 거리, A에서 B까지의 거리 + B 에서 C 까지의 거리 중 더 작은 값이다.
# 문제
11404번 : 플로이드
https://www.acmicpc.net/problem/11404
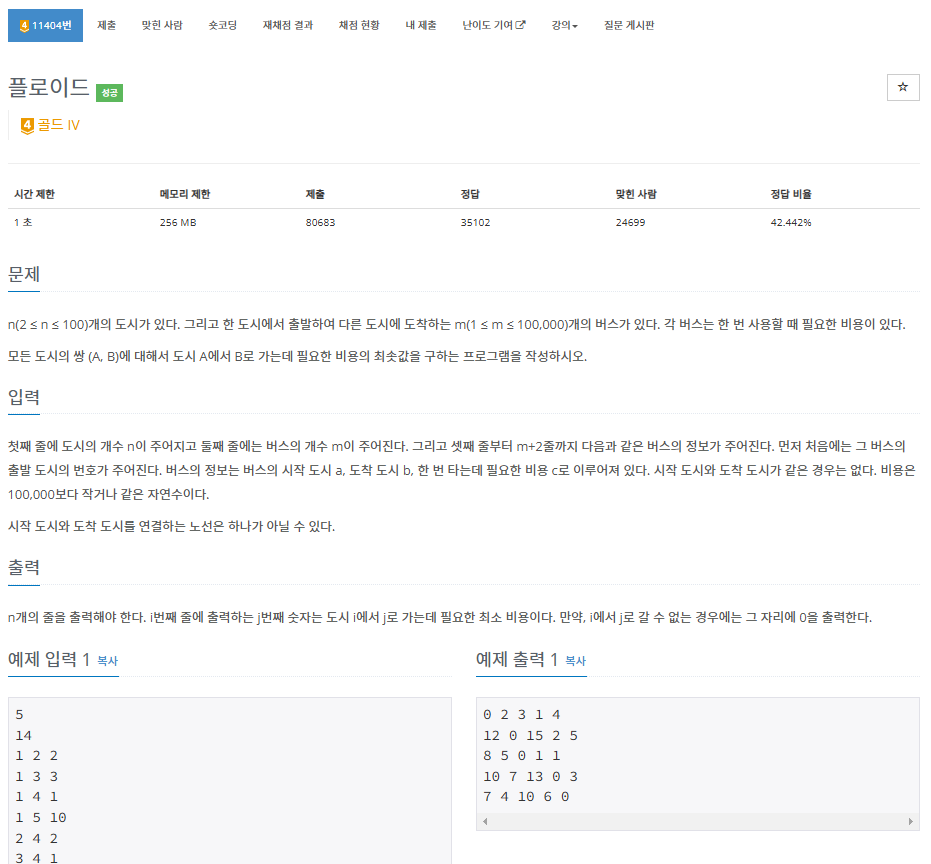
이름도 그냥 플로이드인 문제이다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
// 입력: 도시와 버스의 개수
int cityCount = Integer.parseInt(br.readLine());
int busCount = Integer.parseInt(br.readLine());
// 거리 배열 초기화
int[][] distance = new int[cityCount + 1][cityCount + 1];
final int INF = Integer.MAX_VALUE / 2; // 무한대 값 (오버플로우 방지)
for (int i = 1; i <= cityCount; i++) {
for (int j = 1; j <= cityCount; j++) {
if (i == j) distance[i][j] = 0; // 자기 자신으로 가는 경로는 0
else distance[i][j] = INF; // 초기값은 무한대
}
}
// 입력: 버스 정보 처리
for (int i = 0; i < busCount; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int startCity = Integer.parseInt(st.nextToken());
int endCity = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
// 최소 비용만 저장
distance[startCity][endCity] = Math.min(distance[startCity][endCity], cost);
}
// 플로이드-워셜 알고리즘: 모든 경로에 대한 최소 비용 계산
for (int via = 1; via <= cityCount; via++) { // 경유 도시
for (int from = 1; from <= cityCount; from++) { // 출발 도시
for (int to = 1; to <= cityCount; to++) { // 도착 도시
if (distance[from][to] > distance[from][via] + distance[via][to]) {
distance[from][to] = distance[from][via] + distance[via][to];
}
}
}
}
// 결과 출력: 연결되지 않은 경우 0 출력
for (int i = 1; i <= cityCount; i++) {
for (int j = 1; j <= cityCount; j++) {
if (distance[i][j] == INF) sb.append(0).append(" ");
else sb.append(distance[i][j]).append(" ");
}
sb.append("\n");
}
System.out.println(sb);
}
}3중 for 문을 돌릴때 경유도시가 밖에 있어야 하는것이 중요하다
# 문제
11780번 : 플로이드2
https://www.acmicpc.net/problem/11780

플로이드 워셜 알고리즘에 경로까지 구하는 문제이다.
위 문제와 똑같은 방식으로 구했지만 경로를 List 에 저장하고 만약에 더 짧은 경로를 발견하면
경로를 담은 list 를 갱신하는 방식으로 구현했다. (A -> C 경로는 삭제 하고 A -> C 경로에 A -> B 경로와 B -> C 까지 경로 추가)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
// 입력: 도시와 버스의 개수
int cityCount = Integer.parseInt(br.readLine());
int busCount = Integer.parseInt(br.readLine());
// 거리 배열 초기화
Distance[][] distances = initializeDistances(cityCount);
// 입력: 버스 정보 처리
for (int i = 0; i < busCount; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int startCity = Integer.parseInt(st.nextToken());
int endCity = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
updateDistance(distances, startCity, endCity, cost);
}
// 플로이드-워셜 알고리즘 실행
floydWarshall(distances, cityCount);
// 결과 출력
printResults(distances, cityCount, sb);
System.out.println(sb);
}
// 거리 배열 초기화 메서드
private static Distance[][] initializeDistances(int cityCount) {
final int INF = Integer.MAX_VALUE / 2; // 무한대 값 (오버플로우 방지)
Distance[][] distances = new Distance[cityCount + 1][cityCount + 1];
for (int i = 1; i <= cityCount; i++) {
for (int j = 1; j <= cityCount; j++) {
distances[i][j] = new Distance();
if (i == j) distances[i][j].cost = 0; // 자기 자신으로 가는 경로는 0
else distances[i][j].cost = INF; // 초기값은 무한대
}
}
return distances;
}
// 거리 업데이트 메서드
private static void updateDistance(Distance[][] distances, int startCity, int endCity, int cost) {
if (distances[startCity][endCity].cost > cost) {
distances[startCity][endCity].cost = cost;
distances[startCity][endCity].list.clear();
distances[startCity][endCity].list.add(startCity);
distances[startCity][endCity].list.add(endCity);
}
}
// 플로이드-워셜 알고리즘 메서드
private static void floydWarshall(Distance[][] distances, int cityCount) {
for (int via = 1; via <= cityCount; via++) { // 경유 도시
for (int from = 1; from <= cityCount; from++) { // 출발 도시
for (int to = 1; to <= cityCount; to++) { // 도착 도시
if (distances[from][to].cost > distances[from][via].cost + distances[via][to].cost) {
distances[from][to].cost = distances[from][via].cost + distances[via][to].cost;
// 경로 갱신
List<Integer> newPath = new ArrayList<>(distances[from][via].list);
newPath.addAll(distances[via][to].list.subList(1, distances[via][to].list.size()));
distances[from][to].list = newPath;
}
}
}
}
}
// 결과 출력 메서드
private static void printResults(Distance[][] distances, int cityCount, StringBuilder sb) {
final int INF = Integer.MAX_VALUE / 2;
// 최소 비용 출력
for (int i = 1; i <= cityCount; i++) {
for (int j = 1; j <= cityCount; j++) {
if (distances[i][j].cost == INF) sb.append(0).append(" ");
else sb.append(distances[i][j].cost).append(" ");
}
sb.append("\n");
}
// 경로 출력
for (int i = 1; i <= cityCount; i++) {
for (int j = 1; j <= cityCount; j++) {
if (distances[i][j].cost == INF) {
sb.append(0).append("\n");
} else {
sb.append(distances[i][j].list.size()).append(" ");
for (int k : distances[i][j].list) {
sb.append(k).append(" ");
}
sb.append("\n");
}
}
}
}
}
// 거리와 경로를 저장하는 클래스
class Distance {
int cost;
List<Integer> list;
public Distance() {
this.cost = Integer.MAX_VALUE / 2; // 초기값은 무한대
this.list = new ArrayList<>();
}
}